Makine Öğrenmesi(8/10)

Doğrusal Regresyon

Regresyon

Regresyon terimi, değişkenler arasındaki ilişkiyi bulmaya çalıştığınızda kullanılır.Makine Öğreniminde ve istatistiksel modellemede, bu ilişki gelecekteki olayların sonucunu tahmin etmek için kullanılır.

Doğrusal RegresyonDoğrusal regresyon, veri noktaları arasındaki ilişkiyi bulmak için veriler arasından düz bir çizgi çekmek için kullanılır.Bu çizgi gelecekteki değerleri tahmin etmek için kullanılabilir.

Makine Öğreniminde geleceği tahmin etmek çok önemlidir.

Nasıl çalışır?

Python’un veri noktaları arasında bir ilişki bulma ve doğrusal regresyon çizgisi çizme yöntemleri vardır. Matematik formülleri ile yapmak yerine bu yöntemleri nasıl kullanacağımızı göstereceğiz.
Aşağıdaki örnekte, x ekseni yaşı ve y ekseni hızı temsil eder. 13 arabanın yaşını ve hızını bir gişeden geçerken kaydettik. Topladığımız verilerin doğrusal bir regresyonda kullanılıp kullanılamayacağını görelim

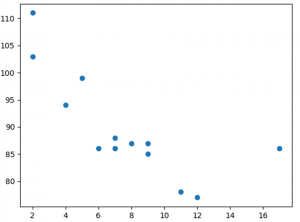
Örnek :

Bir dağılım grafiği çizerek başlayalım:

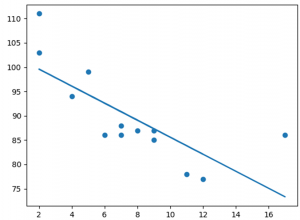
import matplotlib.pyplot as plt

x = [5,7,8,7,2,17,2,9,4,11,12,9,6]

y = [99,86,87,88,111,86,103,87,94,78,77,85,86]

plt.scatter(x, y)

plt.show()

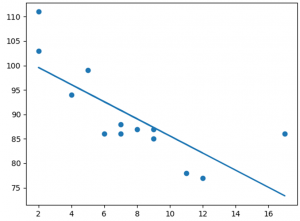
Sonuç:

Örnek :
Scipy'yi importedelim  ve Lineer Regresyon çizgisini çizelim:
İmport matplotlib.pyplot as plt
From scipy import stats
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
slope, intercept, r, p, std_err = stats.linregress(x, y)
def myfunc(x):
return slope * x + intercept
mymodel = list(map(myfunc, x))
 plt.scatter(x, y)
plt.plot(x, mymodel)
plt.show()
Sonuç :

Örneğin Açıklaması 
İhtiyacımız olan modülleri import edelim:
import matplotlib.pyplot as plt
from scipy import stats
x ve y ekseninin değerlerini temsil eden diziler oluşturalım:
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86] 
Doğrusal Regresyon'un bazı önemli anahtar değerlerini döndüren bir metod çalıştıralım:
slope, intercept, r, p, std_err = stats.linregress(x, y)
Yeni bir değer döndürmek için eğim ve kesişim değerlerini kullanan bir fonksiyon oluşturalım. Bu yeni değer, y ekseninde karşılık gelen x değerinin nereye yerleştirileceğini gösterir:
def myfunc(x):
return slope * x + intercept
x dizisinin her değerini fonksiyon aracılığıyla çalıştıralım. Bu, y ekseni için yeni değerlere sahip yeni bir dizi ile sonuçlanır:
mymodel = list(map(myfunc, x))
Orijinal dağılım grafiğini çizelim:
plt.scatter(x, y)
Doğrusal regresyon çizgisini çizelim:
plt.plot(x, mymodel)
 Diyagramı görüntüleyelim:
plt.show()

R-kare:
X ekseninin değerleri ile y ekseninin değerleri arasındaki ilişkinin ne kadar iyi olduğunu bilmek önemlidir, eğer bir ilişki yoksa doğrusal regresyon hiçbir şeyi tahmin etmek için kullanılamaz. 
İlişki, r-kare adı verilen bir değerle ölçülür.R kare değeri 0 ile 1 arasında değişmektedir, burada 0 ilişki yoktur ve 1 %100 ilişkilidir anlamına gelir. 
Python ve Scipy modülü bu değeri sizin için hesaplayacak, tek yapmanız gereken x ve y değerlerini vermek:
Örnek :
Verilerim doğrusal bir regresyona ne kadar iyi uyuyor?

from scipy import stats

x = [5,7,8,7,2,17,2,9,4,11,12,9,6]

y = [99,86,87,88,111,86,103,87,94,78,77,85,86]

slope, intercept, r, p, std_err = stats.linregress(x, y)

print(r)

Çıktı : -0.758591524376155

Not: -0.76 sonucu, mükemmel olmayan bir ilişki olduğunu gösterir, ancak gelecekteki tahminlerde doğrusal regresyon kullanabileceğimizi gösterir.

Gelecekteki Değerleri Tahmin Etme
Şimdi topladığımız bilgileri gelecekteki değerleri tahmin etmek için kullanabiliriz. 
Örnek: 
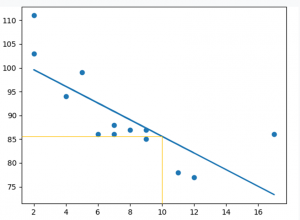
10 yaşında bir arabanın hızını tahmin etmeye çalışalım. Bunu yapmak için yukarıdaki örnekte aynı myfunc () işlevine ihtiyacımız var:
def myfunc(x):
  return slope * x + intercept

Örnek :
10 yaşında bir arabanın hızını tahmin edelim :
from scipy import stats
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
slope, intercept, r, p, std_err = stats.linregress(x, y)
def myfunc(x): 
 return slope * x + intercept
speed = myfunc(10)
print(speed)

Çıktı :85.59308314937454
Örnek, diyagramdan da okuyabileceğimiz bir hız olan 85.6'da öngörülmüştür:

Kötü Uyum?
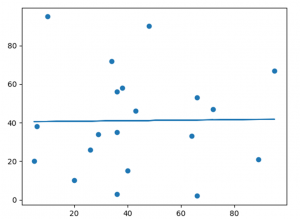
Gelecekteki değerleri tahminetmek için doğrusal regresyonun en iyi yöntem olmayacağı bir örnek oluşturalım.
 x ve y ekseni için bu değerler doğrusal regresyon için çok kötü bir uyum sağlamalıdır:
import matplotlib.pyplot as plt
from scipy import stats
x = [89,43,36,36,95,10,66,34,38,20,26,29,48,64,6,5,36,66,72,40]
y = [21,46,3,35,67,95,53,72,58,10,26,34,90,33,38,20,56,2,47,15]
slope, intercept, r, p, std_err = stats.linregress(x, y)
def myfunc(x): 
 return slope * x + intercept
mymodel = list(map(myfunc, x))
plt.scatter(x, y)
plt.plot(x, mymodel)
plt.show()

Sonuç :

Ve r-kare değeri?
Örnek :
Çok düşük bir r kare değeri almalıyız.
 import numpy
from scipy 
import stats
x = [89,43,36,36,95,10,66,34,38,20,26,29,48,64,6,5,36,66,72,40]
y = [21,46,3,35,67,95,53,72,58,10,26,34,90,33,38,20,56,2,47,15]
slope, intercept, r, p, std_err = stats.linregress(x, y)
print(r)
Çıktı :0.01331814154297491
Sonuç:0.013
 Çok kötü bir ilişki olduğunu gösterir ve bu veri setinin doğrusal regresyon için uygun olmadığını gösterir.

-Burak Can Görgülü